Estimating Curvatures and Their Derivatives on Triangle Meshes

Symposium on 3D Data Processing, Visualization, and Transmission, September 2004

Szymon Rusinkiewicz

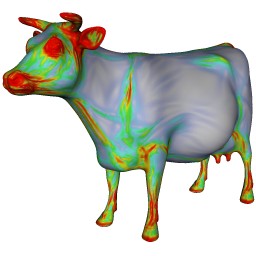Visualization of the curvatures (left) and derivative of curvature (right) estimated on a 3D mesh.

The computation of curvature and other differential properties of surfaces is essential for many techniques in analysis and rendering. We present a finite-differences approach for estimating curvatures on irregular triangle meshes that may be thought of as an extension of a common method for estimating per-vertex normals. The technique is efficient in space and time, and results in significantly fewer outlier estimates while more broadly offering accuracy comparable to existing methods. It generalizes naturally to computing derivatives of curvature and higher-order surface differentials.

PDF File
An earlier version of this paper is available as tech report TR-693-04

The algorithm described in the paper is available as part of the trimesh2 library

Szymon Rusinkiewicz.
"Estimating Curvatures and Their Derivatives on Triangle Meshes."
Symposium on 3D Data Processing, Visualization, and Transmission, September 2004.

@inproceedings{Rusinkiewicz:2004:ECA,
   author = "Szymon Rusinkiewicz",
   title = "Estimating Curvatures and Their Derivatives on Triangle Meshes",
   booktitle = "Symposium on 3D Data Processing, Visualization, and Transmission",
   year = "2004",
   month = sep
}