Schelling Points on 3D Surface Meshes
ACM Transactions on Graphics (Proc. SIGGRAPH), August 2012
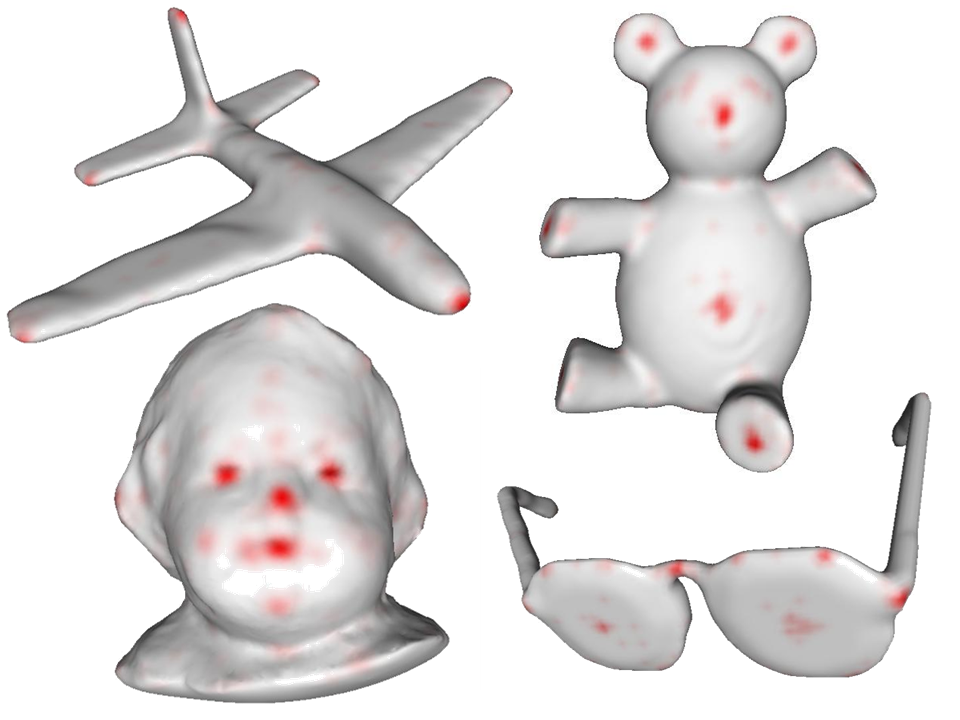 Schelling points (red). Positions on a surface selected consistently by many people when trying to match each other without communication.
Schelling points (red). Positions on a surface selected consistently by many people when trying to match each other without communication.
Abstract
This paper investigates "Schelling points" on 3D meshes, feature
points selected by people in a pure coordination game due to their
salience. To collect data for this investigation, we designed an online experiment that asked people to select points on 3D surfaces
that they expect will be selected by other people. We then analyzed
properties of the selected points, finding that: 1) Schelling point
sets are usually highly symmetric, and 2) local curvature properties (e.g., Gauss curvature) are most helpful for identifying obvious
Schelling points (tips of protrusions), but 3) global properties (e.g.,
segment centeredness, proximity to a symmetry axis, etc.) are required to explain more subtle features. Based on these observations,
we use regression analysis to combine multiple properties into an
analytical model that predicts where Schelling points are likely to
be on new meshes. We find that this model benefits from a variety
of surface properties, particularly when training data comes from
examples in the same object class.
Files
Additional Links
Citation
Xiaobai Chen, Abulhair Saparov, Bill Pang, and Thomas Funkhouser.
"Schelling Points on 3D Surface Meshes."
ACM Transactions on Graphics (Proc. SIGGRAPH), August 2012.
BibTeX
@article{Chen:2012:SPO,
author = "Xiaobai Chen and Abulhair Saparov and Bill Pang and Thomas Funkhouser",
title = "Schelling Points on {3D} Surface Meshes",
journal = "ACM Transactions on Graphics (Proc. SIGGRAPH)",
year = "2012",
month = aug
}