Fuzzy Geodesics and Consistent Sparse Correspondences For Deformable Shapes
Computer Graphics Forum (Symposium on Geometry Processing), July 2010
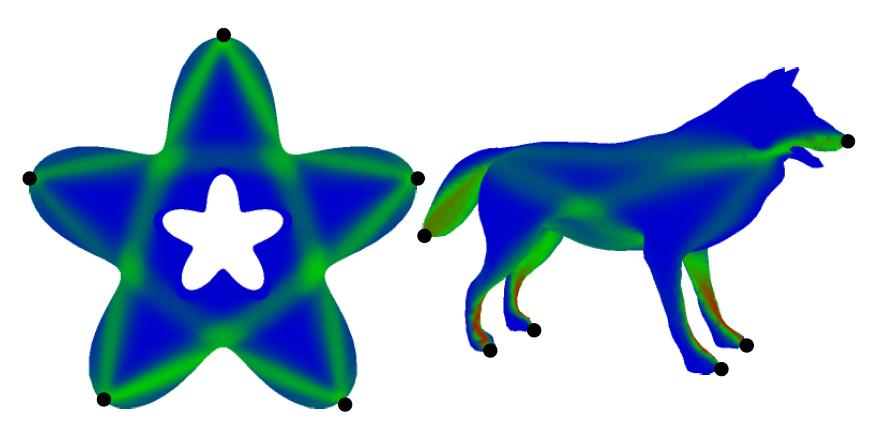
The sum of the fuzzy geodesics between all pairs of marked points
Abstract
A geodesic is a parameterized curve on a Riemannian manifold governed by a second order partial differential
equation. Geodesics are notoriously unstable: small perturbations of the underlying manifold may lead to dramatic
changes of the course of a geodesic. Such instability makes it difficult to use geodesics in many applications,
in particular in the world of discrete geometry. In this paper, we consider a geodesic as the indicator function of
the set of the points on the geodesic. From this perspective, we present a new concept called fuzzy geodesics and
show that fuzzy geodesics are stable with respect to the Gromov-Hausdorff distance. Based on fuzzy geodesics, we
propose a new object called the intersection configuration for a set of points on a shape and demonstrate its effectiveness
in the application of finding consistent correspondences between sparse sets of points on shapes differing
by extreme deformations.
Links
Citation
Jian Sun, Xiaobai Chen, and Thomas Funkhouser.
"Fuzzy Geodesics and Consistent Sparse Correspondences For Deformable Shapes."
Computer Graphics Forum (Symposium on Geometry Processing) 29(5), July 2010.
BibTeX
@article{Sun:2010:FGA,
author = "Jian Sun and Xiaobai Chen and Thomas Funkhouser",
title = "Fuzzy Geodesics and Consistent Sparse Correspondences For Deformable
Shapes",
journal = "Computer Graphics Forum (Symposium on Geometry Processing)",
year = "2010",
month = jul,
volume = "29",
number = "5"
}